跳跃表的结构实现上，借鉴了链表的思想，在数据节点上同时记录的前进和后退节点的指针，当然还远远不止于此，每个数据节点还需要记录每次跳过多个节点后指向跳表节点的多级指针，由于每个节点存储的数据都事先经过了排序，结合每个节点上的“跳跃指针”，可以快速定位到需要查询的节点。

结构

Redis 中的跳跃表分为跳跃表节点（zskiplistNode）和跳跃表主体（zskiplist）两部分：

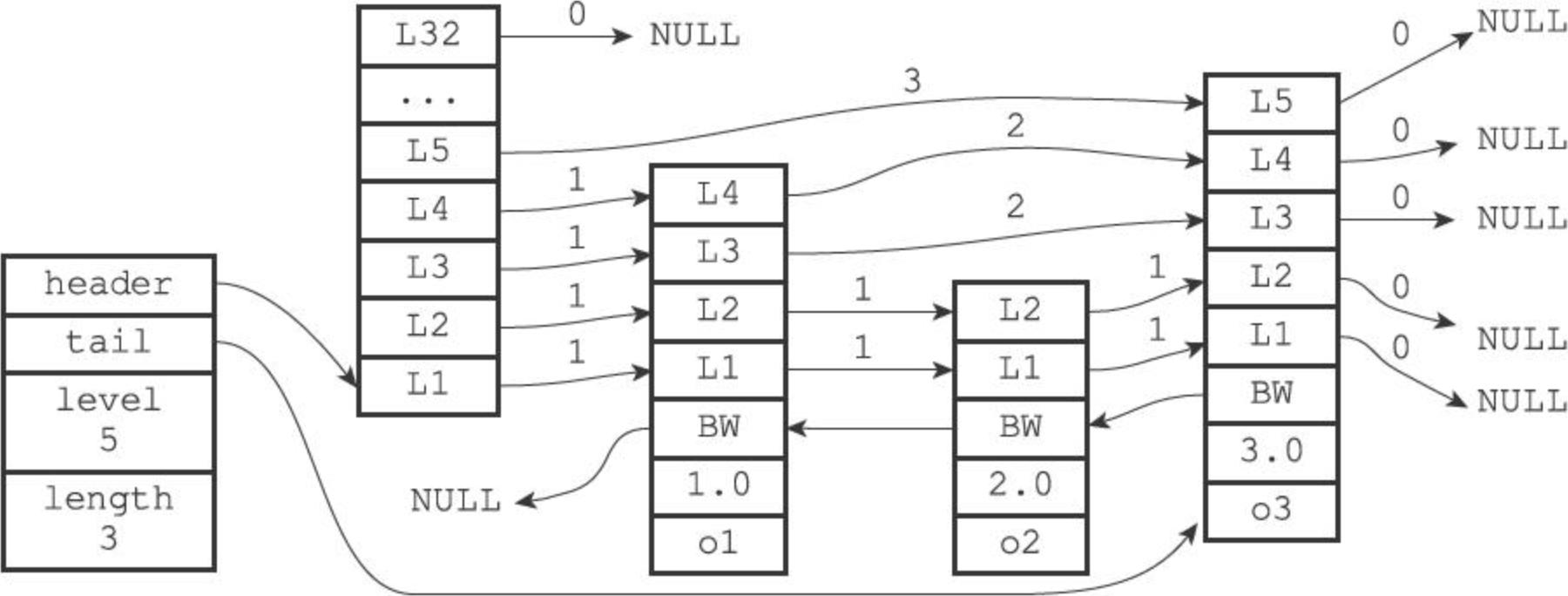
zskiplistNode 节点的定义如下（https://github.com/redis/redis/blob/7.2.4/src/server.h#L1336）：

typedef struct zskiplistNode {
    // 数据值，是个SDS
    sds ele;
    // 分值，排序用到
    double score;
    // 回退指针
    struct zskiplistNode *backward;
    // 多层指针
    struct zskiplistLevel {
        // 前进指针
        struct zskiplistNode *forward;
        // 跨度值
        unsigned long span;
    } level[];
} zskiplistNode;

其中 zskiplistLevel->span 为每个指针指向的节点距离当前节点的跨度值，用于评估指向节点和当前节点的远近。

zskiplist 结构体的构成：

typedef struct zskiplist {
    // 头尾指针
    struct zskiplistNode *header, *tail;
    // skiplistNode的数量
    unsigned long length;
    // 子节点中指针的最高层数
    int level;
} zskiplist;

操作

创建

在初始化创建一个跳跃表时候，表头节点会默认创建一个 ZSKIPLIST_MAXLEVEL=32 层的多层指针：

zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

查询

skiplist 查询时候主要思路是从头结点开始，按照 level 指针从高层到底层的顺序依次遍历，如果没有找到想要的节点，就查看 forward 指针的元素，如果没有 forward 则 level - 1 进入下一层遍历，直至最终匹配到对应元素或者到达尾部元素，skiplist 提供了两个 API 用于查询节点元素：

• zslGetRank：通过 score 分值获取元素的排名（从1开始）：

unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    x = zsl->header;

    // 从头结点开始，按照level从高到低顺序遍历
    for (i = zsl->level-1; i >= 0; i--) {
        // forward和预期不符，就累加span到rank中
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                sdscmp(x->level[i].forward->ele,ele) <= 0))) {
            rank += x->level[i].span;
            x = x->level[i].forward;
        }

        // 多层遍历的终止条件，最终命中预期score
        if (x->ele && x->score == score && sdscmp(x->ele,ele) == 0) {
            return rank;
        }
    }
    return 0;
}

• zslGetElementByRank：通过从1开始的排名值 rank 获取元素内容：

zskiplistNode* zslGetElementByRank(zskiplist *zsl, unsigned long rank) {
    zskiplistNode *x;
    // 记录一个遍历的排序值
    unsigned long traversed = 0;
    int i;

    x = zsl->header;
    // 从头结点的最高level层开始，层层遍历前进
    for (i = zsl->level-1; i >= 0; i--) {
        // 计算当前节点rank，不符合预期就继续前进
        while (x->level[i].forward && (traversed + x->level[i].span) <= rank)
        {
            traversed += x->level[i].span;
            x = x->level[i].forward;
        }

        // 终止条件，最终获得的rank和预期一致，表明找到了对应的节点
        if (traversed == rank) {
            return x;
        }
    }
    return NULL;
}

插入

zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        /* store rank that is crossed to reach the insert position */
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* we assume the element is not already inside, since we allow duplicated
     * scores, reinserting the same element should never happen since the
     * caller of zslInsert() should test in the hash table if the element is
     * already inside or not. */
    level = zslRandomLevel();
    if (level > zsl->level) {
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level;
    }
    x = zslCreateNode(level,score,ele);
    for (i = 0; i < level; i++) {
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

        /* update span covered by update[i] as x is inserted here */
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
}

可以看出 skiplist 插入时候的逻辑还是比较复杂的，这部分逻辑也是跳跃表的精髓，归纳起来，redis 跳跃表插入的逻辑有这么几个要点：

• 初始化了两个数组，update[ZSKIPLIST_MAXLEVEL] 记录每个level层遍历时候跳跃到下一层前经过的节点，这部分节点也就是后续需要和新节点重新更新关联关系的节点。rank[ZSKIPLIST_MAXLEVEL] 用来记录遍历每层level时候跳跃到下一层前经过的总跨度，例如 rank[i] 就表示从 header 节点开始查找到 update[i] 节点时候进过的 span 之和；

• 首先通过遍历查找的方法，按照level从高层到底层，逐层对比查找新节点在跳跃表中合适的位置，并且更新填充 update 和 rank 数组；

• 对要插入的新节点随机生成一个多层数组 level，然后根据已经得到的 update 和 rank 数组的信息更新新节点的 level 数组中每一层的 forward 和 span，再将新节点重新和 update 数组中的每个节点建立指针关联；

• skiplist 之所以要对新插入的节点随机生成 level 层级，是为了节省计算量，如果每次对所有层级都更新一遍，可能会影响性能，通过随机算法，只对低于随机层高的级数更新索引，有效节省了计算量。

skiplist 通过 zslRandomLevel() 函数为新节点生成随机层高：

int zslRandomLevel(void) {
    static const int threshold = ZSKIPLIST_P*RAND_MAX;
    int level = 1;
    while (random() < threshold)
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

其中随机概率因子 ZSKIPLIST_P=0.25，这个函数返回 i 层高度的概率可以通过以下公式计算：

P(i)=(1-p(i-1))*0.25，其中P(1)=0.25，1<=i<=ZSKIPLIST_MAXLEVEL

删除

skiplist 删除节点时候，同样需要记录每层抵达指定节点时候经过的跳变节点清单 update，执行删除操作之前，需要更新所有 update 清单中的 forward 指针和 span 值：

int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. */
    x = x->level[0].forward;
    if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
        zslDeleteNode(zsl, x, update);
        if (!node)
            zslFreeNode(x);
        else
            *node = x;
        return 1;
    }
    return 0; /* not found */
}

void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            update[i]->level[i].span -= 1;
        }
    }
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
    zsl->length--;
}